How To Draw 3d Vectors On Paper
7. Vectors in 3-D Space
We saw earlier how to represent 2-dimensional vectors on the ten-y plane.
Now we extend the idea to represent three-dimensional vectors using the x-y-z axes. (See The 3-dimensional Co-ordinate System for background on this).
Case
The vector OP has initial point at the origin O (0, 0, 0) and terminal point at P (two, 3, v). We tin can draw the vector OP equally follows:
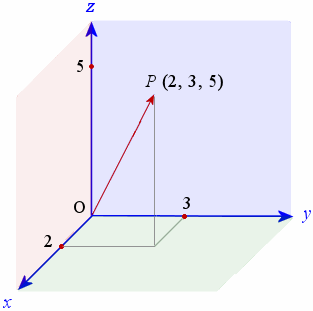
Magnitude of a 3-Dimensional Vector
We saw earlier that the distance between two points in 3-dimensional space is
`"distance"\ AB = ` `sqrt ((x_2-x_1)^ii+ (y_2-y_1)^2+ (z_2-z_1)^two)`
For the vector OP above, the magnitude of the vector is given by:
`| OP | = sqrt(2^ii+ iii^2+ five^2) = half dozen.sixteen\ "units" `
Adding 3-dimensional Vectors
Earlier we saw how to add 2-dimensional vectors. We at present extend the thought for 3-dimensional vectors.
We simply add together the i components together, so the j components and finally, the k components.
Example 1

Two anchors are holding a ship in place and their forces acting on the ship are represented by vectors A and B as follows:
A = twoi + fivej − ivk and B = −2i − 3j − 5k
If we were to replace the 2 anchors with 1 single anchor, what vector represents that unmarried vector?
Answer
Dot Production of iii-dimensional Vectors
To find the dot product (or scalar product) of 3-dimensional vectors, we but extend the ideas from the dot product in two dimensions that we met earlier.
Case 2 - Dot Product Using Magnitude and Bending
Find the dot product of the vectors P and Q given that the angle betwixt the two vectors is 35° and
| P | = 25 units and | Q | = iv units
Answer
Instance 3 - Dot Production if Vectors are Multiples of Unit Vectors
Find the dot product of the vectors A and B (these come from our anchor example to a higher place):
A = 2i + fivej − 4k and B = −iii − threej − fivek
Answer
Direction Cosines
Suppose we have a vector OA with initial point at the origin and final point at A.
Suppose also that nosotros have a unit vector in the same direction equally OA. (Go hither for a reminder on unit vectors).
Let our unit vector be:
u = u 1 i + u ii j + u 3 m
On the graph, u is the unit vector (in black) pointing in the same management as vector OA, and i, j, and k (the unit vectors in the x-, y- and z-directions respectively) are marked in green.
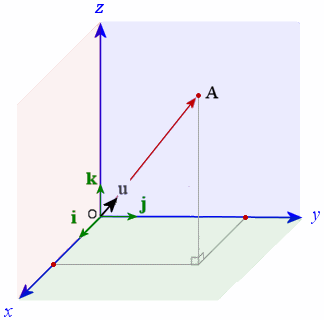
We now zoom in on the vector u, and change orientation slightly, every bit follows:
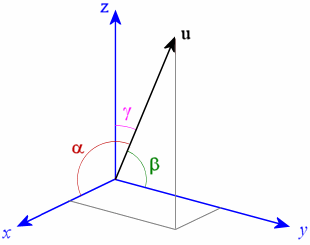
At present, if in the diagram to a higher place,
α is the angle between u and the x-axis (in night red),
β is the angle between u and the y-axis (in green) and
γ is the bending between u and the z-axis (in pinkish),
and then we tin use the scalar production and write:
u one
= u • i
= 1 × i × cos α
= cos α
u 2
= u• j
= 1 × 1 × cos β
= cos β
u three
= u • k
= ane × 1 × cos γ
= cos γ
So we can write our unit vector u as:
u = cos α i + cos β j + cos γ thou
These three cosines are called the direction cosines.
Angle Between 3-Dimensional Vectors
Before, we saw how to detect the angle between 2-dimensional vectors. We employ the same formula for iii-dimensional vectors:
`theta=arccos((P * Q)/(|P||Q|))`
Example 4
Discover the angle between the vectors P = 4i + 0j + sevenk and Q = -iii + j + 3k .
Answer
Exercise
Find the angle between the vectors P = 3i + fourj − 7g and Q = -2i + j + 3k .
Respond
Application
We have a cube ABCO PQRS which has a string forth the cube's diagonal B to S and another along the other diagonal C to P
What is the bending betwixt the 2 strings?
Answer
Problem Solver
Need help solving a different Graphing problem? Effort the Problem Solver.
Disclaimer: IntMath.com does not guarantee the accuracy of results. Problem Solver provided by Mathway.
Source: https://www.intmath.com/vectors/7-vectors-in-3d-space.php
Posted by: keatonpausay.blogspot.com


0 Response to "How To Draw 3d Vectors On Paper"
Post a Comment